Comparing-Players-in-Fifa-18
Identifying comparable players by attributes in the Fifa 18 video game
Comparing Players in Fifa 18
Ariel Aguilar Gonzalez
This purpose of this project is to compare players by attributes in the Fifa 18 video game. The full interactive visualization can be seen here. The code below demonstrates how I prepared and cleaned the Fifa 18 data. Code written in R.
The Fifa 18 players database is available through Kaggle, and includes almost 18,000 players with 185 fields for each player including about 36 player attributes, such as finishing and crossing.
#-------------------------------#
# Import Data & Libraries #
#-------------------------------#
library("dplyr")
library("readr")
library("rvest")
library("purrr")
library("stringr")
library("tidyr")
library("highcharter")
library("ggplot2")
library("htmltools")
library("ggdendro")
player_raw <- read_csv(".../Kaggle Dataset.csv")
# 17,994 players
# 185 attributes
#-------------------------------#
# Data Validation #
#-------------------------------#
# Check that non-English letters in player names are read in correctly
player_raw$name[1:50]
# First 50 names looks good, different character accents are read in correctly
num_cols <- sapply(player_raw, is.numeric)
player_num <- player_raw[,num_cols]
summary(player_num)
# All of the attribute variables are on a scale of 0-100
# height_cm, weight_kg are clean
# there's also ratings for each outfield position (seperate for gks)
# stick to player preferences to describe position
#-------------------------------#
# Data Cleaning #
#-------------------------------#
# Any NA values?
anyNA(player_raw)
# True
# How many rows contain NA values?
nrow(player_raw[rowSums(is.na(player_raw)) > 0,])
# 17,994, all of them
# Which columns contain NA values?
colnames(player_raw)[colSums(is.na(player_raw)) > 0]
# Club/League (Free Agents)
# Release Clause (Possible)
# And position variables
# Drop these position variables will use preferences for position
position_cols <- colnames(player_raw)[colSums(is.na(player_raw)) > 0][-c(1,2,3,4)]
player_df <- player_raw[, !(colnames(player_raw) %in% position_cols)]
# Now how many rows contain NA values?
nrow(player_df[rowSums(is.na(player_df)) > 0,])
# 1,494, much less
# Select which columns to keep
colnames(player_df)
# Investigate columns which contain "prefers", "speciality", and "trait"
df_traits <- player_df[1:25, grepl("prefers|speciality|trait", colnames(player_df))]
# Binary variables, drop "speciality" and "trait" columns
player_slim <- player_df[, !grepl("speciality|trait", colnames(player_df))]
# Now at 94 columns
# Convert player_pref to clean position columns
player_pref <- player_slim[,grepl("prefers", colnames(player_slim))]
# Binary encode player preferences
for (i in 1:ncol(player_pref)){
player_pref[,i] <- ifelse(player_pref[,i] == "False",0,1)
}
# Find out the largest number of positions a single player is associated with
max(rowSums(player_pref))
# 4
# Create player positions dataframe
player_positions <- data.frame(matrix(data = NA, nrow = nrow(player_pref), ncol = 4))
# Extract each player's position preference, up to a max of four positions
for (i in 1:nrow(player_pref)){
positions <- gsub("prefers_", "", colnames(player_pref)[(player_pref[i,]) == 1])
for (j in 1:length(positions)){
player_positions[i,j] <- positions[j]
}
}
# Rename columns
new_positions <- c("position_1", "position_2", "position_3", "position_4")
colnames(player_positions) <- new_positions
# Replace position preference cols with new position cols
player_slim2 <- cbind(player_slim[, !grepl("prefers", colnames(player_slim))], player_positions)
# Limit to identifing varibles, attributes and position variables
player_final <- player_slim2[, c(1,2,4,10,11,16,20,34:71)]
# 45 columns, 36 different attributes for each player
# Clean up the photo column
urlimage_path <- "https://cdn.sofifa.org/18/players/"
player_final$photo <- gsub(urlimage_path, "", player_final$photo)
# Clean up the environment
rm(player_df, player_raw, player_slim, player_slim2, player_positions, player_num,
df_traits, player_pref)
It’s possible to compare players across all of these attributes, however I’d like to create a visualization showing each player and their relative distance to each other in terms of similarity.
Using principal component analysis (PCA), I compressed the 36 player attributes (plus height and weight) to two components.
#-------------------------------#
# Dimensionality Reduction #
#-------------------------------#
# Use pca to reduce attributes down to two dimensions
attribute_cols <- colnames(player_final)[c(4:5,8:41)]
# Any NA in attributes?
anyNA(player_final[,attribute_cols])
# False
# Scale variables before applying tsne
# Focus on the top 750 players in the world, according to Fifa 18
data_scaled = apply(player_final[1:750,attribute_cols], 2, function(r) {
if (sd(r) != 0)
res = (r - mean(r))/sd(r) else res = 0 * r
res
})
pc <- prcomp(data_scaled)
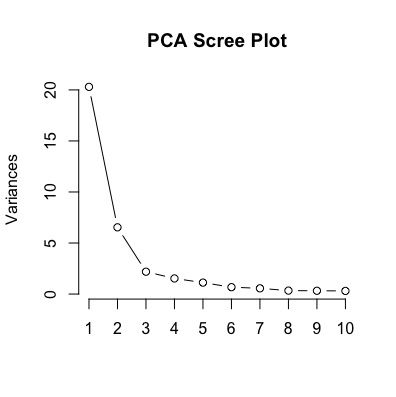
plot(pc, type='l',main = "PCA Scree Plot")
summary(pc)
# About 75% of variance captured in first two components
pc_df <- cbind.data.frame(pc$x[,1], pc$x[,2])
The scree plot below shows that the two components account for 75% of the variance in the 36 player attributes. Ideally, at least 85% of the variance would be retained, but according to the scree plot that would require about four components. For the purposes of visualization, I’ll limit the number of components to two.
With the player attributes condensed to just two dimensions, its straightforward to create a scatter plot where each point represents a single player. For the plot below and the rest of the analysis, I focus on the top 750 players by overall ranking in the Fifa dataset.
ggplot(pc_df, aes(pc$x[,1], pc$x[,2])) +
geom_point() +
ggtitle("Player Attributes Condensed by Principal Components") +
ylab("Principal Component #2") +
xlab("Principal Component #1") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))
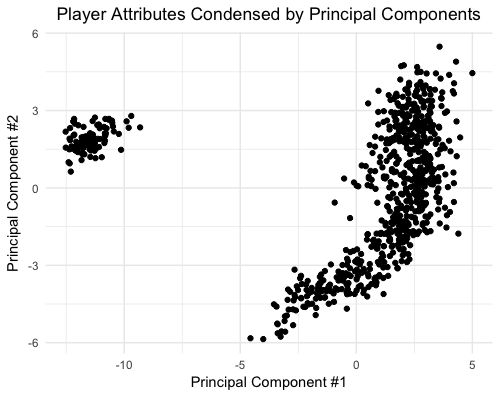
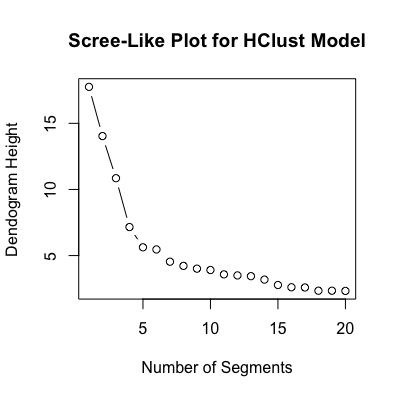
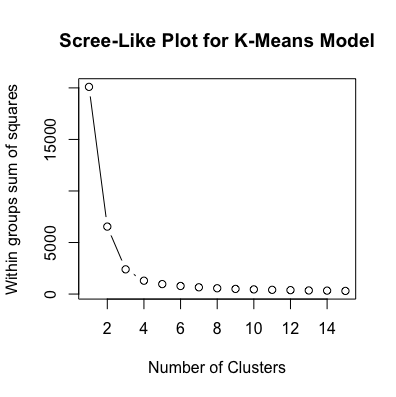
It’s clear that there are some groups of players clustered together. It’s likely that goalkeepers form the cluster of players on the left of the scatter plot given that their attributes are so different to outfield players. To identify other potential clusters, I utilized both K-Means and Hierarchical Agglomerative (HClust) clustering. As the scree-like plots below indicate, each of the algorithms suggest a different number of clusters (judging by the “elbow” of each plot). The Hierarchical method suggests four or five clusters, while looking at the within group sum of squares for K-Means suggest three clusters would be optimal.
#-------------------------------#
# Clustering Analysis #
#-------------------------------#
## Hierarchical Clustering
d <- dist(pc_df, method = "euclidean")
fit <- hclust(d, method="complete")
# Plot the height of the dendogram over the number of segments in the dendogram
# Focus on the first 20 values since the height decreases asymptotically after that
plot(seq(1,20), sort(fit$height, decreasing = TRUE)[1:20], type = "b",
ylab = "Dendogram Height", xlab = "Number of Segments",
main = "Scree-Like Plot for HClust Model")
# Looks like 4 forms the elbow of the plot, segment where the longest jump takes place
hclust_groups <- cutree(fit, k=5) # cut tree into 5 clusters
## K-Means Clustering
# Determine number of clusters
wss <- (nrow(pc_df)-1)*sum(apply(pc_df,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(pc_df,iter.max = 1000,nstart = 25,
centers=i)$withinss)
plot(1:15, wss, type="b", xlab="Number of Clusters",
ylab="Within groups sum of squares", main = "Scree-Like Plot for K-Means Model")
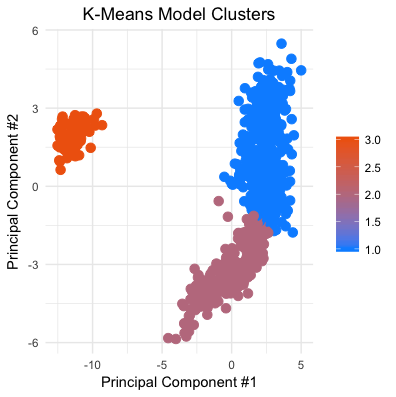
Running each of the HClust and K-Means models on the Fifa players scatterplot shows the differences between the two models. K-Means operates on the assumption of equally proportionate clusters, and this bias shows in the plots below.
k <- kmeans(pc_df, 3, nstart=25, iter.max=1000)
## Compare the clusters graphically
cluster_data <- cbind(pc_df, hclust_groups, k$cluster)
ggplot(cluster_data, aes(pc$x[,1], pc$x[,2], color = hclust_groups)) +
geom_point(size=3) +
ggtitle("Hclust Model Clusters") +
ylab("Principal Component #2") +
xlab("Principal Component #1") +
theme_minimal() +
scale_color_gradient(low = "#0091ff", high = "#f0650e") +
theme(plot.title = element_text(hjust = 0.5),
legend.title = element_blank())
ggplot(cluster_data, aes(pc$x[,1], pc$x[,2], color = k$cluster)) +
geom_point(size=3) +
ggtitle("K-Means Model Clusters") +
ylab("Principal Component #2") +
xlab("Principal Component #1") +
theme_minimal() +
scale_color_gradient(low = "#0091ff", high = "#f0650e") +
theme(plot.title = element_text(hjust = 0.5),
legend.title = element_blank())
# Prefer hclust method b/c it does not assume that the clusters should be proportionate
# in size, would expect gk's to form a small seperate group in our data
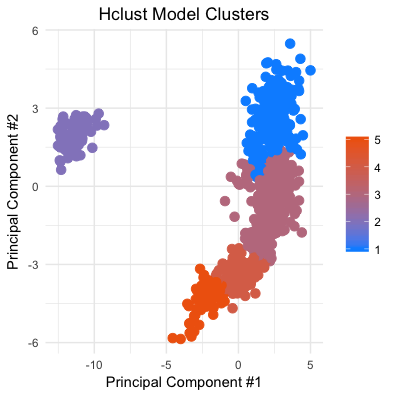
I used these clusters to identify the player “type”, a more general classification than a player’s position. However, I can take advantage of the player position variable to help “profile” each cluster.
As it turns out, the cluster on the far left is indeed composed entirely of goalkeepers. The lowermost cluster is composed almost entirely of center-backs(CBs), with one center defensive midfield (CDM), and two right backs (RBs). This cluster forms the “Defensive Anchor” type. The next cluster moving up the right-hand side, consists mostly of CBs, with some CDMs and central midfielders (CMs). I call this cluster the “Defensive Playmaker” type and includes players like David Luiz and Nemanja Matic. The next pinkish cluster, is the largest cluster and contains a wide mix of defenders, midfielders and forwards. I think of this cluster as a catch-all for players who don’t fall in the other clusters, I use the term “Box to Box Player” to describe this cluster, but it includes players as varying as N’golo Kante and Zlatan Ibrahimovic. Finally, the blue cluster at the top has players such as Neymar and Lionel Messi. I call this cluster the “Out and Out Attacker” type.
#-------------------------------#
# Cluster Profiles #
#-------------------------------#
player_profile <- cbind(player_final[1:750, !(colnames(player_final) %in% attribute_cols)],
cluster_data[,1:3])
colnames(player_profile)[10:11] <- c("x", "y")
# Look at each cluster by player position and overall rating
# note that its only postion_1 so not complete picture but approximate
table(player_profile$hclust_groups, player_profile$position_1)
# Group 1 comprised mostly of STs, wingers and some midfielders (blue), out and out attackers
# Group 2 comprised of all goalkeepers (purple), goalkeepers
# Group 3 big range of midfielders (largest group), strikers and defenders (pink), all-rounders
# Group 4 contains mostly CBs, with some CMs and CDMs (orange-pink), defensive playmaker
# Group 5 comprised of almost all CBs, and one CDM, two RBs (orange), defensive anchor
overall_profile <- player_profile %>%
group_by(hclust_groups) %>%
summarise(min = min(overall),
median = median(overall),
mean = mean(overall),
max = max(overall))
# Evenly distributed amongst overall
# Set cluster colours
player_profile$color <- ifelse(player_profile$hclust_groups == 1, "#2C90F7",
ifelse(player_profile$hclust_groups == 2, "#9487C6",
ifelse(player_profile$hclust_groups == 3, "#C07C8D",
ifelse(player_profile$hclust_groups == 4, "#DC7157",
"#EF6537"))))
# Rename cluster groups
player_profile$hclust_groups <- ifelse(player_profile$hclust_groups == 1, "Out and Out Attacker",
ifelse(player_profile$hclust_groups == 2, "Goalkeeper",
ifelse(player_profile$hclust_groups == 3, "Box to Box Player",
ifelse(player_profile$hclust_groups == 4, "Defensive Playmaker",
"Defensive Anchor"))))
# Rename hclust_group column
colnames(player_profile)[12] <- c("type")
# Combine position columns
player_profile$position_2 <- ifelse(is.na(player_profile$position_2), "", player_profile$position_2)
player_profile$position_3 <- ifelse(is.na(player_profile$position_3), "", player_profile$position_3)
player_profile$position_4 <- ifelse(is.na(player_profile$position_4), "", player_profile$position_4)
player_profile$position <- ifelse(nchar(player_profile$position_4) > 0, paste(player_profile$position_1,
player_profile$position_2,
player_profile$position_3,
player_profile$position_4, sep = ","),
ifelse(nchar(player_profile$position_3) > 0,paste(player_profile$position_1,
player_profile$position_2,
player_profile$position_3, sep = ","),
ifelse(nchar(player_profile$position_2) > 0,paste(player_profile$position_1,
player_profile$position_2, sep = ","),
player_profile$position_1)))
player_profile$position <- toupper(player_profile$position)
# Drop old position columns
player_profile <- player_profile[, !(colnames(player_profile) %in% new_positions)]
#-------------------------------#
# Nearest Neighbours #
#-------------------------------#
# Distance Matrix
dist_df <- as.matrix(d)
# Create dataframe for loop results
nearest_neigh <- data.frame(matrix(data = NA, nrow = nrow(player_profile), ncol = 5))
for (i in 1:nrow(player_profile)){
# Find the five smallest distances for each row
# Ignore the smallest b/c that will just be the diagonal value
all_dist <- dist_df[i,]
dist_cols <- colnames(dist_df)
dist_df2 <- data.frame(all_dist, dist_cols)
dist_order <- dist_df2 %>%
arrange(all_dist)
dist_order$dist_cols <- as.numeric(levels(dist_order$dist_cols))[dist_order$dist_cols]
# Get the row indices of the five nearest players
five_ind <- dist_order[2:6, "dist_cols"]
# Get names of the five nearest players
five_names <- player_profile[five_ind, "name"]
# Store names in empty dataframe
for (j in 1:length(five_names)){
nearest_neigh[i,j] <- five_names[j]
}
}
colnames(nearest_neigh) <- c("neigh_1", "neigh_2", "neigh_3", "neigh_4", "neigh_5")
player_complete <- cbind(player_profile, nearest_neigh)
# Export
write.csv(player_complete, "Fifa_18_Player_Profiles.csv")